고정 헤더 영역
상세 컨텐츠
본문
안녕하세요 이번에는 bra-ket 표현방법을 실전에 한번 적용해보도록 하겠습니다. 먼저 아래에 암모니아 분자가 있다고 가정해 봅니다. 그리고 암모니아 분자는 진동, 회전등을 하지 않아 진동과 회전에 의한 상태는 없고 Fig 1에서처럼 대칭인 상태만 존재한다고 가정해 봅시다. 즉 암모니아 분자는 수소원자가 이루는 평면 기준으로 질소원자의 위 혹은 아래 위치에 따른 두 가지 상태밖에 없다고 가정한 상황입니다. 또한 어떠한 외부 에너지 없이 아래 두 상태는 오로지 터널링에 의해서 변한다고 가정하겠습니다.
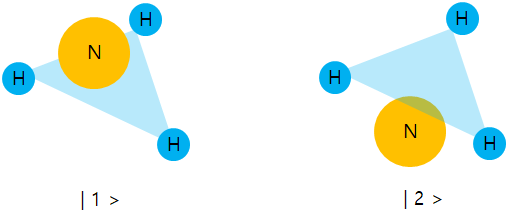
Fig 1의 왼쪽 그림에서 처럼 질소 원자가 수소원자들이 이루는 평면 위에 위치한 상태를 | 1 >, 오른쪽 그림에서 처럼 질소 원자가 수소원자들이 이루는 평면 아래에 위치한 상태를 | 2 >이라고 하겠습니다. 즉 상태 | 1 >과 | 2 >는 암모니아 분자의 기반 상태가 되는 것입니다. 암모니아 분자의 상태가 | 1 > 혹은 | 2 > 둘 중 하나인 상태 일 수도 있겠지만 두 기반 상태가 동시에 존재하여 조합으로도 암모니아의 상태를 표현할 수 있습니다. 그래서 암모니아 상태를 ψ라고 했을 때 bra-ket 표현방법을 써서 아래와 같이 표현이 가능합니다.
| ψ > = | 1 >< 1 | ψ > + | 2 >< 2 | ψ >
위 식을 해석하자면 상태 ψ는 상태 ψ가 기반상태 | 1 >인 상황과 상태 ψ가 기반상태 | 2 >인 상황의 조합이라고 해석할 수 있습니다. 상태 ψ가 기반상태 | 1 >밖에 가질 수 없는 경우엔 | ψ > = | 1 >< 1 | ψ > 이라고 쓸 수 있습니다. 한 가지만 더 짚고 넘어가자면 상태 ψ가 기반상태 | 1 >밖에 가질 수 없는 경우를 왜 | ψ > = < 1 | ψ >>이라고 표현하지 않는지 궁금해하시는 분도 계실 겁니다.
이유는 | ψ > 이라는 표현 자체가 완전한 표현이 아니기 때문입니다. 최종 상태 χ까지 넣어서 < χ | ψ >라고 써줘야 초기 상태 ψ에서 최종 상태 χ가 되는 상황을 완전하게 표현할 수 있습니다. 최종 상태 χ를 | ψ > = | 1 >< 1 | ψ >에 적용하면 < χ | ψ > = < χ | 1 >< 1 | ψ> 이 되어 비로소 완전한 표현을 할 수 있는 것입니다. | ψ >라는 표현은 계산의 중간과정이라고 생각하시면 됩니다.
끝.
'양자역학' 카테고리의 다른 글
| 에너지띠(energy band)의 형성 (0) | 2021.01.10 |
|---|---|
| 양자역학에서 기반상태 (base state) (0) | 2020.12.13 |
| Quantum dot 이해하기 (quantum confinement effect) (0) | 2020.12.07 |
| bra-ket 사용법 (0) | 2020.12.05 |
| 터널링 효과 (tunneling effect) (0) | 2020.11.21 |





댓글 영역