고정 헤더 영역
상세 컨텐츠
본문
오늘은 양자역학에서 등장하는 기반 상태 (base state)에 대해서 이야기를 해볼까 합니다. 먼저 기반 상태의 정의는 어떠한 상태를 이루는 더 이상 하위 단계로 분해될 수 없는 상태를 말합니다. 이렇게 말하면 이해가 되지 않기 때문에 직교 좌표계로 예를 들어보겠습니다. 양자역학의 기반상태는 x, y, z 직교 좌표계에서 등장하는 단위 벡터와도 같습니다. x,y,z 직교좌표를 이루는 가장 기본적인 벡터는 x, y, z단위 벡터로 직교 좌표계에서는 단위 벡터를 다른 벡터의 조합으로 표현할 수 없습니다. 그리고 각각의 단위 벡터에 계수를 곱하면 x, y, z 직교 좌표계에서 어떠한 벡터든 표현이 가능합니다. 원점으로부터 점(1, 2, 3)을 가리키는 벡터 A는 단위 벡터와 계수의 조합으로 아래와 같이 표현 가능합니다.
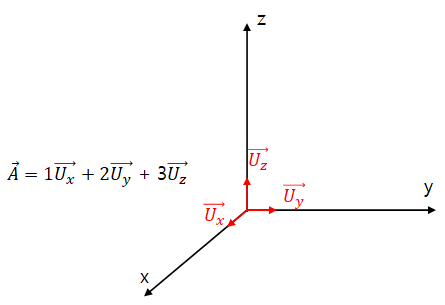
직교좌표계에서 단위 벡터와 계수의 조합으로 어떠한 벡터를 나타내듯이 양자역학에서는 기반 상태와 계수의 조합으로 어떠한 상태를 표현합니다. 수소원자에 상태가 ψ인 전자가 있습니다. 전자의 상태ψ는 운동량과 전자의 스핀으로 표현 가능하고, 이때 기반상태는 운동량 값 하나하나에 대응되는 값과 스핀에 해당하는 값입니다. 예를 들어 전자가 가질 수 있는 운동량의 값이 1, 3, 5, 7, 10이라면 운동량과 관련된 기반 상태는 5개이고 전자는 z 축 기준으로 up spin과 down spin을 가질 수 있으므로 z 축 기준으로 스핀에 관련된 기반 상태는 2개입니다. 전자의 상태 ψ는 이러한 기반 상태들의 조합으로 표현 될 수 있습니다.

전자가 일정한 운동량을 갖지 않는 상태도 얼마든지 표현이 가능합니다. 예를 들어 전자가 운동량을 1도 가질 수 있고 3도 가질 수 있는 상태라면, 운동량이 1인 기반 상태와 운동량이 3인 기반 상태에 적절한 계수를 사용한 조합(중첩)으로 전자의 상태 ψ를 표현 가능합니다. 스핀도 마찬가지입니다. 각각의 up spin 과 down spin의 기반 상태에 적절한 계수를 사용하여 두 기반 상태를 조합(중첩)하면 일정한 스핀을 갖지 않는 전자의 상태 ψ를 표현 가능합니다.
끝.
'양자역학' 카테고리의 다른 글
| 에너지띠(energy band)의 형성 (0) | 2021.01.10 |
|---|---|
| Bra-ket 실전 적용 (0) | 2020.12.22 |
| Quantum dot 이해하기 (quantum confinement effect) (0) | 2020.12.07 |
| bra-ket 사용법 (0) | 2020.12.05 |
| 터널링 효과 (tunneling effect) (0) | 2020.11.21 |





댓글 영역